Besluiten over het gebruik van drinkwaternetten worden veelal gebaseerd op simulaties. Ze gaan echter voor een groot deel voorbij aan de onzekerheden in diverse invoeren van deze modellen. In dit artikel worden een benadering (probabilistische simulaties), een softwarebibliotheek en een bureaubladapplicatie gepresenteerd, die het mogelijk maken om de hydraulische simulaties uit te voeren met inbegrip van diverse onzekerheden.
Download hier de pdf van dit artikel.
Geschreven door Mark Morley, Peter van Thienen, Ina Vertommen (KWR Water Research Institute), Mollie Torello & Dragan Savić (KWR, University of Exeter, VK )
Besluitvorming over de aanleg, de uitbreiding, de renovatie, de operatie en het beheer van drinkwaterleidingnetten wordt voor een aanzienlijk deel gebaseerd op hydraulische simulaties. Hiermee voorspelt een computer of er, gegeven een beschrijving van het netwerk, de operatie hiervan en de watervraag, aan alle klanten voldoende water met voldoende druk wordt geleverd. Veelgebruikte voorbeelden zijn EPANET [1], InfoWorks [2] en WaterGEMS [3]. Bij het maken van deze modellen en het nemen van beslissingen voor waterdistributienetwerken wordt meestal gewerkt met een aanpak waarbij één set gegevens – materialen, diameters, lengtes en verbondenheid van leidingen, watervraagpatronen, ingaande druk of pompsturing - leidt tot één uitkomst – een voorspelde druk en volumestroom overal in het netwerkmodel. Het maakt niet uit hoe vaak het softwaremodel wordt uitgevoerd, met dezelfde invoer is de uitkomst altijd hetzelfde. Dit wordt de deterministische aanpak genoemd. Maar er zijn nog veel onzekerheden, zowel over de toestand van het netwerk als over hoe het precies werkt (zie als illustratie de grote variatie in gemeten drukken op dezelfde weekdag op dezelfde tijdstippen in afbeelding 1). Deze onzekerheden hebben te maken met dingen als de werkelijke diameter van de leidingen, die door degradatie kleiner kan worden of in het verleden verkeerd kan zijn geregistreerd, het soms slecht bijhouden van installatie- en verbindingsgegevens, en de hoeveelheden water die gebruikers nodig hebben.
Hoewel in modellen normaal gesproken wordt aangenomen dat de watervraag op elk moment van de dag en elke dag van de week bekend is, is het niet mogelijk om precies te weten hoeveel water de gebruikers afnemen. Normaal gesproken worden deze onzekerheden in het besluitvormingsproces op twee manieren meegenomen. Enerzijds door het netwerkmodel te kalibreren: wandruwheids- (en eventueel aanvullende) parameters worden zodanig bijgesteld dat de gesimuleerde drukken goed overeenkomen met gemeten drukken. Dit geeft echter geen garanties voor het correct functioneren buiten het bereik van de kalibratiecondities en ‘masseert’ alle afwijkingen in werkelijke parameterwaarden ten opzichte van die in het model weg in de gekozen kalibratieparameters. Anderzijds worden verschillende scenario’s overwogen om een paar mogelijke situaties te simuleren, maar dit aantal is praktisch gezien beperkt.
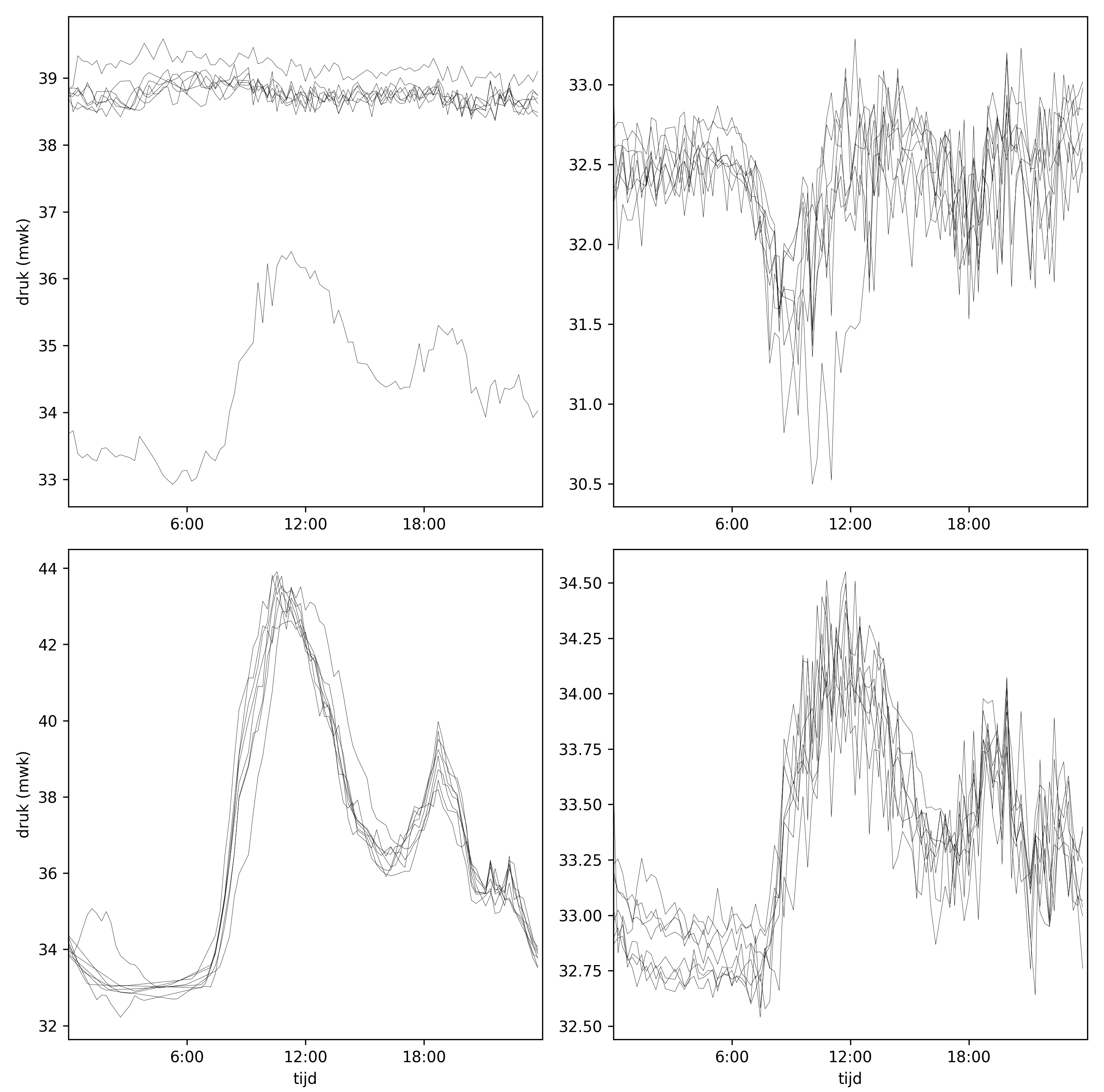
Afbeelding 1. Drukmetingen op vier punten in eenzelfde distributiegebied, op acht opeenvolgende zondagen in 2017 (databron: Evides)
Hoewel dit in het verleden onhaalbaar was, maakt de rekenkracht die tegenwoordig beschikbaar is het ook mogelijk al deze onzekerheden mee te nemen in de berekeningen. Het meenemen van al deze onzekerheden wordt de probabilistische benadering genoemd. Deze is heel vergelijkbaar met de manier waarop weersvoorspellingen tegenwoordig vaak van ‘pluimen’ zijn voorzien, die de bandbreedte van de te verwachten condities weergeven. Hoewel er in de wetenschappelijke literatuur veel interesse is in probabilistische modellen [4], waren er tot voor kort nog geen softwaretools om deze aanpak te ondersteunen.
In dit artikel wordt VlinderNET gepresenteerd, samen met de onderliggende PHS-softwarebibliotheek, die het voor gebruikers mogelijk maken om probabilistische leidingnetberekeningen uit te voeren. In het artikel wordt toegelicht hoe dit werkt, worden enkele voorbeelden van rekenresultaten in vergelijking met traditionele, deterministische resultaten gegeven, en wordt een perspectief geschetst voor brede toepassing van probabilistisch rekenen in het modelleren van leidingnetten.
Probabilistische Hydraulische Simulatie en software-implementatie
Om probabilistische netwerkberekeningen mogelijk te maken, is de PHS-bibliotheek ontwikkeld. Dit is een softwarebibliotheek die bedoeld is als onderdeel van een beslissingsondersteunend systeem of om de deterministische simulatie van een hydraulische tool, zoals EPANET, te vervangen of aan te vullen. De bibliotheek is in programmeertaal C++ geschreven en is daarnaast ook aan te roepen vanuit Python en R.
Met de bibliotheek kunnen complexe kansverdelingen worden ingesteld voor verschillende numerieke invoerparameters in het hydraulische model. Voorbeelden zijn de vraag naar water, de diameter en de wandruwheid van leidingen en de status van leidingen en afsluiters. Het is ook mogelijk om aparte verdelingen toe te passen op specifieke onderdelen van het netwerk of groepen onderdelen, op basis van bepaalde criteria. Zo kunnen bijvoorbeeld verschillende verouderingsregimes worden toegepast op leidingen van verschillende materialen en leeftijden.
Het probabilistische model gebruikt de kansverdelingen om op gestructureerde wijze een breed scala aan willekeurige invoerwaarden te genereren, passend bij de voorgeschreven kansverdelingen, voor opeenvolgende parallelle (lokale of cloudgebaseerde) hydraulische simulaties. Voor elk van deze combinaties van invoerwaarden worden hydraulische simulaties uitgevoerd met een aangepaste versie van de open-source EPANET-hydraulische solver (die is uitbreid met drukgestuurde modellering om lekkages te simuleren). Hierbij worden eenvoudige statistieken (minimum, maximum, gemiddelde, mediaan, modus) en een histogram voor elk resultaat opgeslagen. Sommige probabilistische resultaten (zoals vraag, druk, volumestroom, enz.) zijn ook tijdsafhankelijk. Daarom worden deze statistieken en histogrammen voor elke tijdstap in het model bijgehouden.
VlinderNET
Met de PHS-bibliotheek als basis is een gebruiksvriendelijke bureaubladapplicatie gebouwd, VlinderNET, die alle probabilistische simulatiefunctionaliteiten op eenvoudige wijze toegankelijk maakt voor gebruikers. Deze kan in plaats van EPANET of andere hydraulische software worden ingezet. VlinderNET biedt onder andere de volgende functionaliteiten: import van hydraulische netwerken in de vorm van EPANET-invoerbestanden, visualisatie bovenop OpenStreetMap-kaarten, definitie van kansverdelingen voor alle onzekere parameters in het netwerk, toepassing van kansverdelingen op elementen van het netwerk, uitvoeren van deterministische en probabilistische berekeningen, en visualisatie van de resultaten hiervan, inclusief een vergelijking van de twee (deterministische en probabilistische) simulaties naast elkaar.
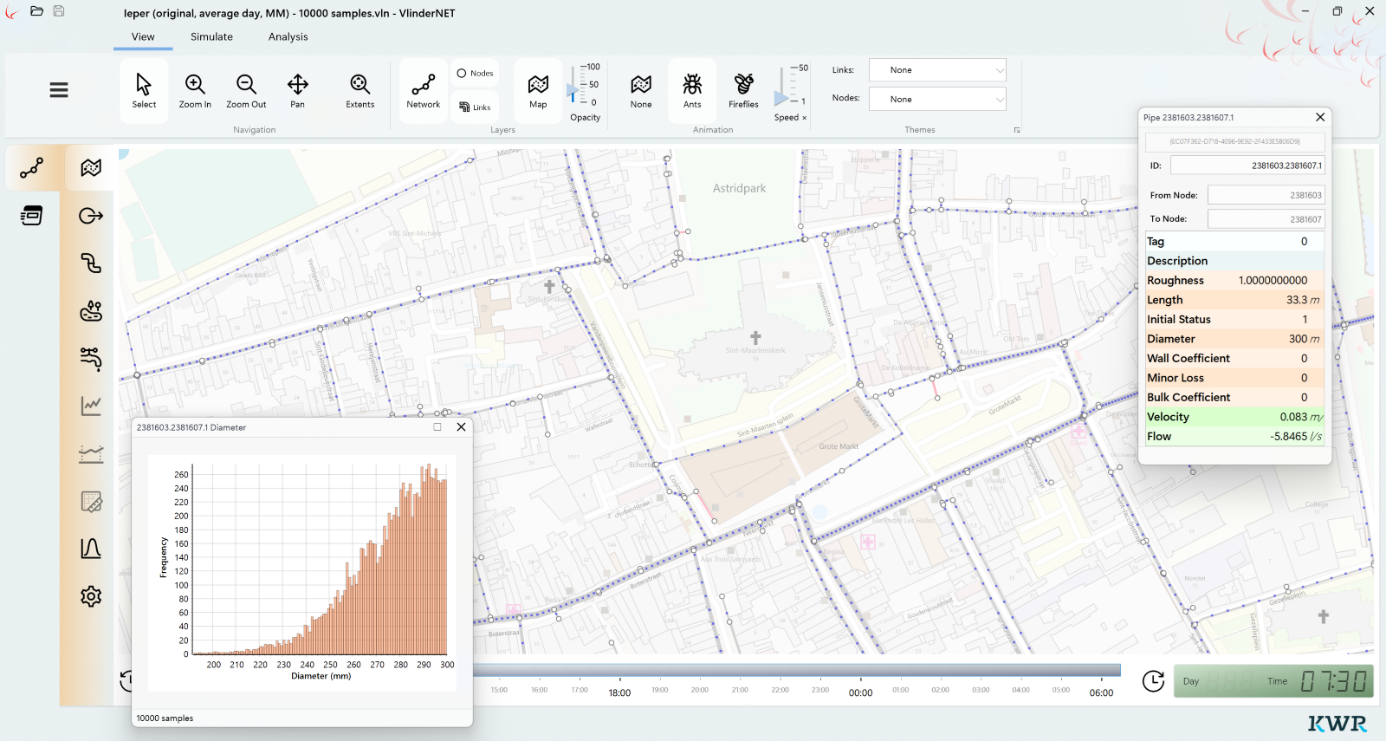
Afbeelding 2. Grafische gebruikersinterface van VlinderNET
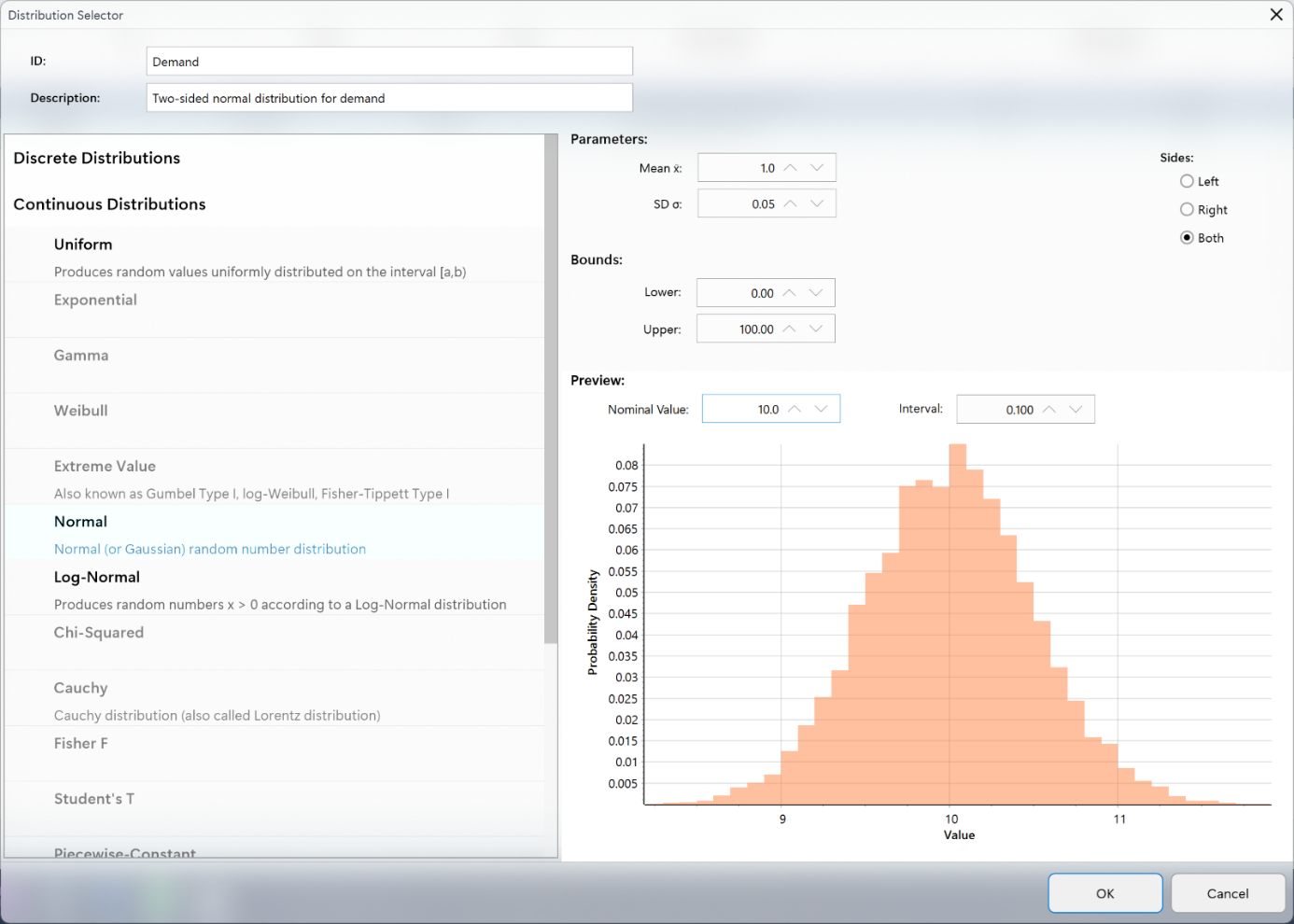
Afbeelding 3. Definitie van een kansverdeling in VlinderNET
Simulaties van een bestaand en een geoptimaliseerd netwerk
Om de prestaties van de PHS-bibliotheek en de VlinderNET-tool te testen en om te begrijpen hoe onzekerheid de werking van een echt leidingnetmodel beïnvloedt, is de toepassing getest op het netwerkmodel van Ieper (België), geleverd door het lokale waterbedrijf, De Watergroep. Hiervan waren twee varianten beschikbaar: 1) de bestaande structuur zoals deze in de grond ligt, en 2) een door KWR voorgesteld netwerkontwerp. Dat laatste werd geoptimaliseerd om een beter gestructureerd ontwerp te bereiken met lussen en vertakkingen. Hiermee kunnen kosten worden verlaagd en de waterkwaliteit verbeterd, terwijl rekening wordt gehouden met minimale druk, maximale sectiegrootte (in aantal aansluitingen in een vertakte lengte), brandweeromstandigheden en leveringszekerheid [5].
Omdat er geen gegevens van De Watergroep beschikbaar waren om de degradatie van de leidingen te modelleren, zijn hiervoor enkele aannames gemaakt: leidingen kunnen door corrosie kleiner worden dan hun nominale diameter, maar niet groter. Watervraag kan daarentegen zowel kleiner als groter worden dan de nominale waarde.
Volumestroom en druk
In afbeelding 4 wordt een voorbeeld van een simulatieresultaat van het bovengenoemde netwerk getoond. Hierin is de kansverdeling weergegeven (met kleur; blauw is een grote kans, wit is een kleine kans, de blauwgrijze lijnen geven de randen van gesimuleerde waarden weer), voor de volumestroom door een enkele buis in het netwerkmodel als functie van de tijd, met de gemiddelde waarde weergegeven als stippellijn. Ter vergelijking is ook het resultaat van een deterministische simulatie weergegeven (doorgetrokken blauwe curve), uiteraard niet als kansverdeling maar als enkele curve.
De belangrijkste boodschap van deze afbeelding is dat voor plausibele invoerwaarden (binnen realistische onzekerheidsmarges) het bereik waarbinnen resulterende volumestromen te verwachten zijn, behoorlijk groot is. In dit geval kan bij een deterministische waarde van 5 liter per seconde een realistisch bereik van 0,5 tot meer dan 10 L/s horen. Dit betekent dat het werkelijke debiet bijna zeker geen 5 liter zal zijn, maar ergens tussen 0,5 en 10 liter, met een kleinere kans dichter bij deze randwaarden.
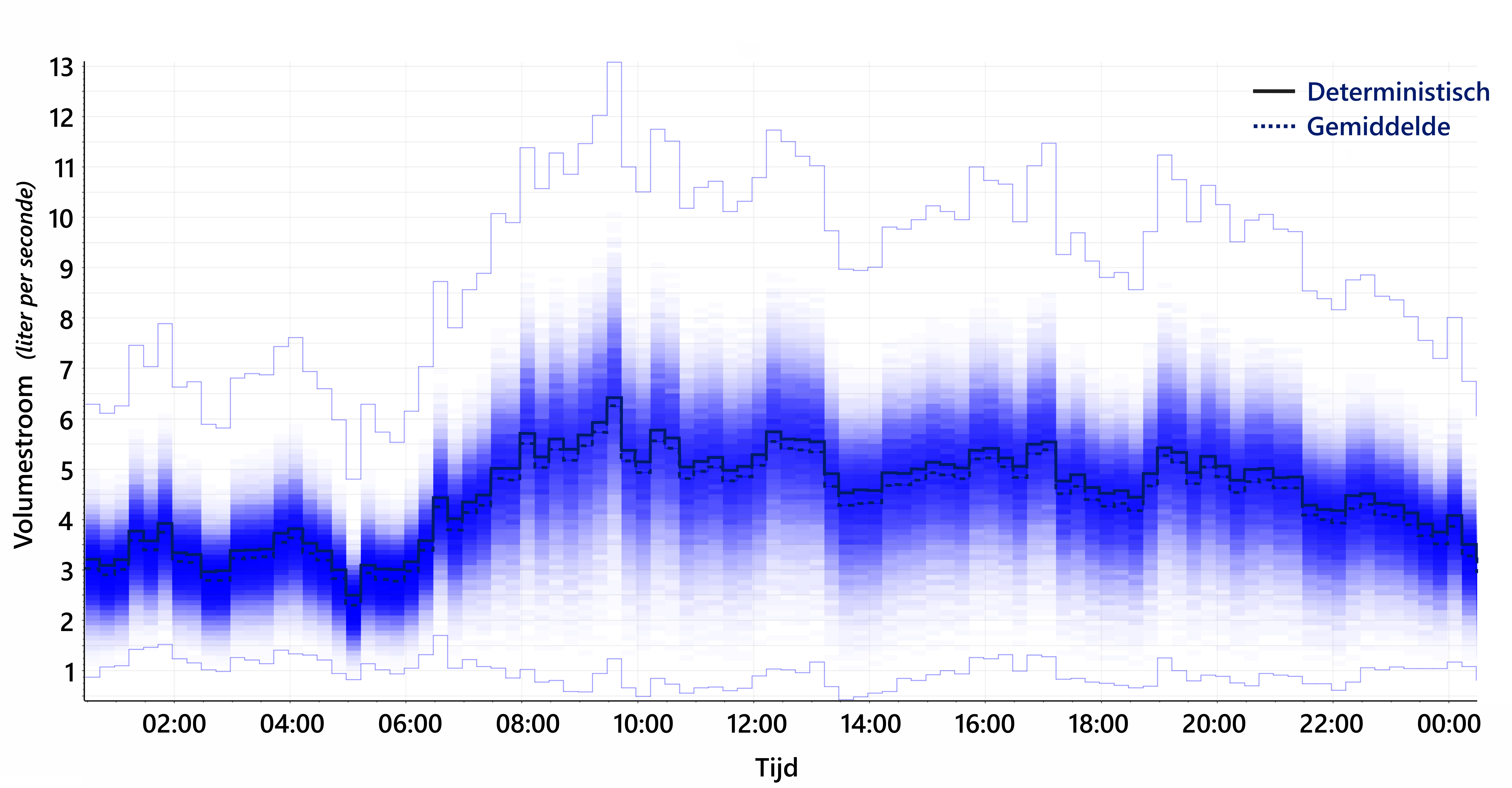
Afbeelding 4. Voorbeeld van probabilistische volumestroomvoorspelling in een enkele leiding van het netwerk van Ieper als functie van de tijd, met een deterministische voorspelling ter vergelijking
Op eenzelfde manier wordt de onzekerheid in de druk in het netwerk geïllustreerd in afbeelding 5. Opnieuw geeft een donkerdere kleur een grotere kans aan, de stippellijn de gemiddelde waarde uit de probabilistische simulaties, en de doorgetrokken lijn de deterministisch bepaalde waarde. Ook hier is een aanzienlijk bereik van mogelijke drukken te zien vergeleken met de met een deterministische simulatie bepaalde waarde die normaal gesproken wordt gebruikt. Merk op dat, voor druk, de waargenomen relatieve variatie aanzienlijk kleiner is, met een maximale variatie tussen probabilistische drukken van ongeveer 1 meter stijghoogte, in vergelijking met de variatie in de volumestroom.
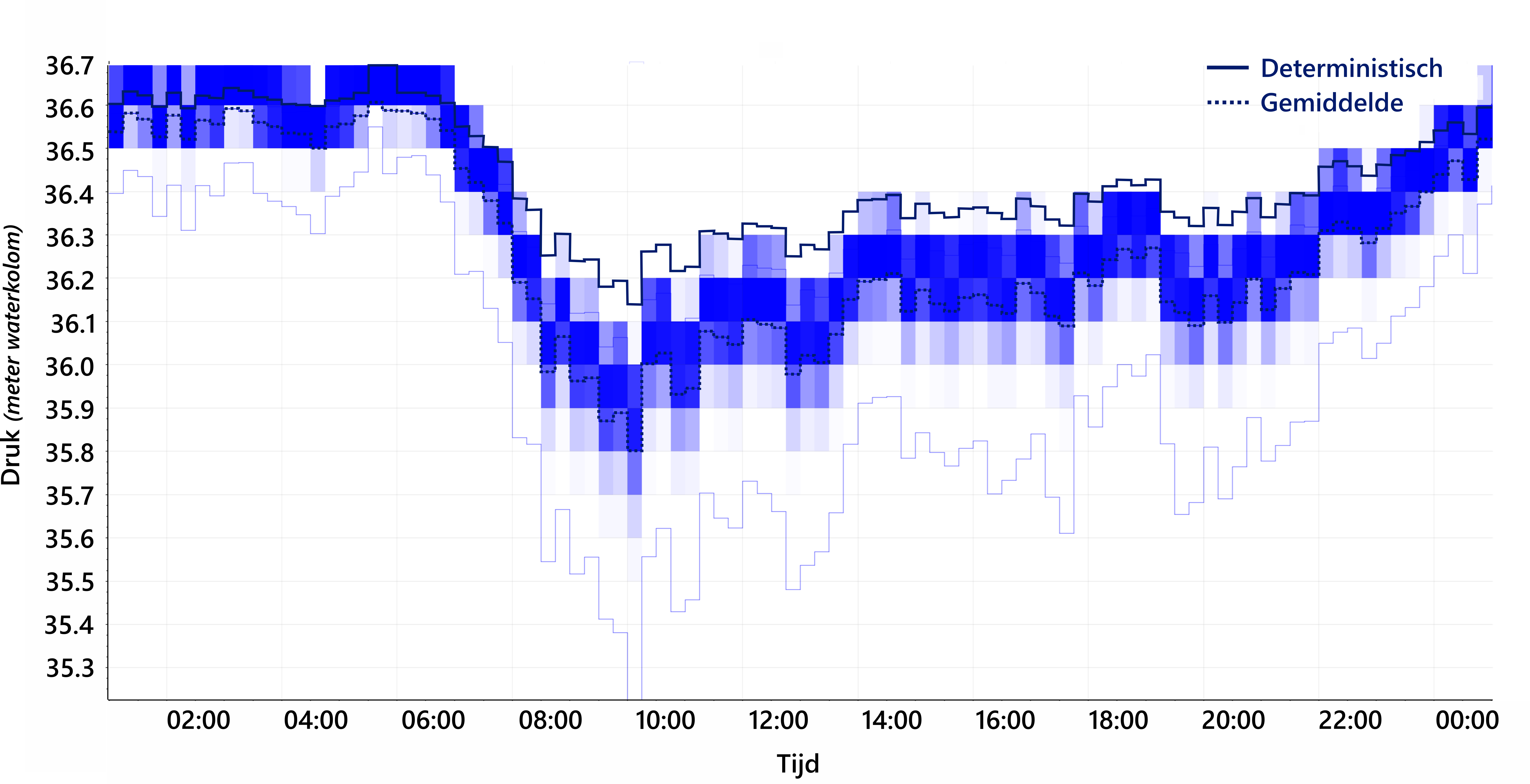
Afbeelding 5. Voorbeeld van probabilistische drukvoorspelling in een enkele leiding van het netwerk van Ieper als functie van de tijd, met een deterministische voorspelling ter vergelijking
Volumestroom en druk zijn feitelijk de belangrijkste en meest gebruikte parameters voor operationele en strategische beslissingen in en over het leidingnet. Inzicht in hun onzekerheid kan bijdragen aan betere beslissingen met een grotere kans op succes.
Andere parameters
Naast volumestroom en druk zijn met een leidingnetmodel ook andere parameters te berekenen die van belang zijn voor operationele en strategische beslissingen en die zeer gevoelig kunnen zijn voor onzekerheden in de invoer van het leidingnetmodel. Een voorbeeld is de verblijftijd van het water. Deze parameter wil men vaak niet al te ver laten oplopen vanwege de mogelijkheid van nagroei van micro-organismen. Afbeelding 6 laat zien hoe deze parameter kan variëren in het bestaande netwerk (blauw) en het geoptimaliseerde netwerk (rood; let op dat dit netwerk is geoptimaliseerd op minimaal volume, niet op verblijftijd). Opnieuw is een relatief grote mate van onzekerheid te zien in de brede marges die zijn berekend voor de verblijftijd.
Hoewel de stromingsomstandigheden tussen de twee modellen (bestaand en geoptimaliseerd) niet sterk variëren onder onzekere omstandigheden, laat de verblijftijd duidelijk zien hoe de prestaties van het netwerk voorspelbaarder worden in de geoptimaliseerde vorm (afbeelding 7). Deze afbeelding toont een leiding waarbij de probabilistische variatie (rode bandbreedte) veel kleiner is wanneer geoptimaliseerd is dan wanneer dit niet is gebeurd (blauwe bandbreedte). Dit is te verwachten als je bedenkt dat er in het geoptimaliseerde model minder wegen beschikbaar zijn door het netwerk vanwege het verkleinen en sluiten van leidingen als onderdeel van het optimalisatieproces.
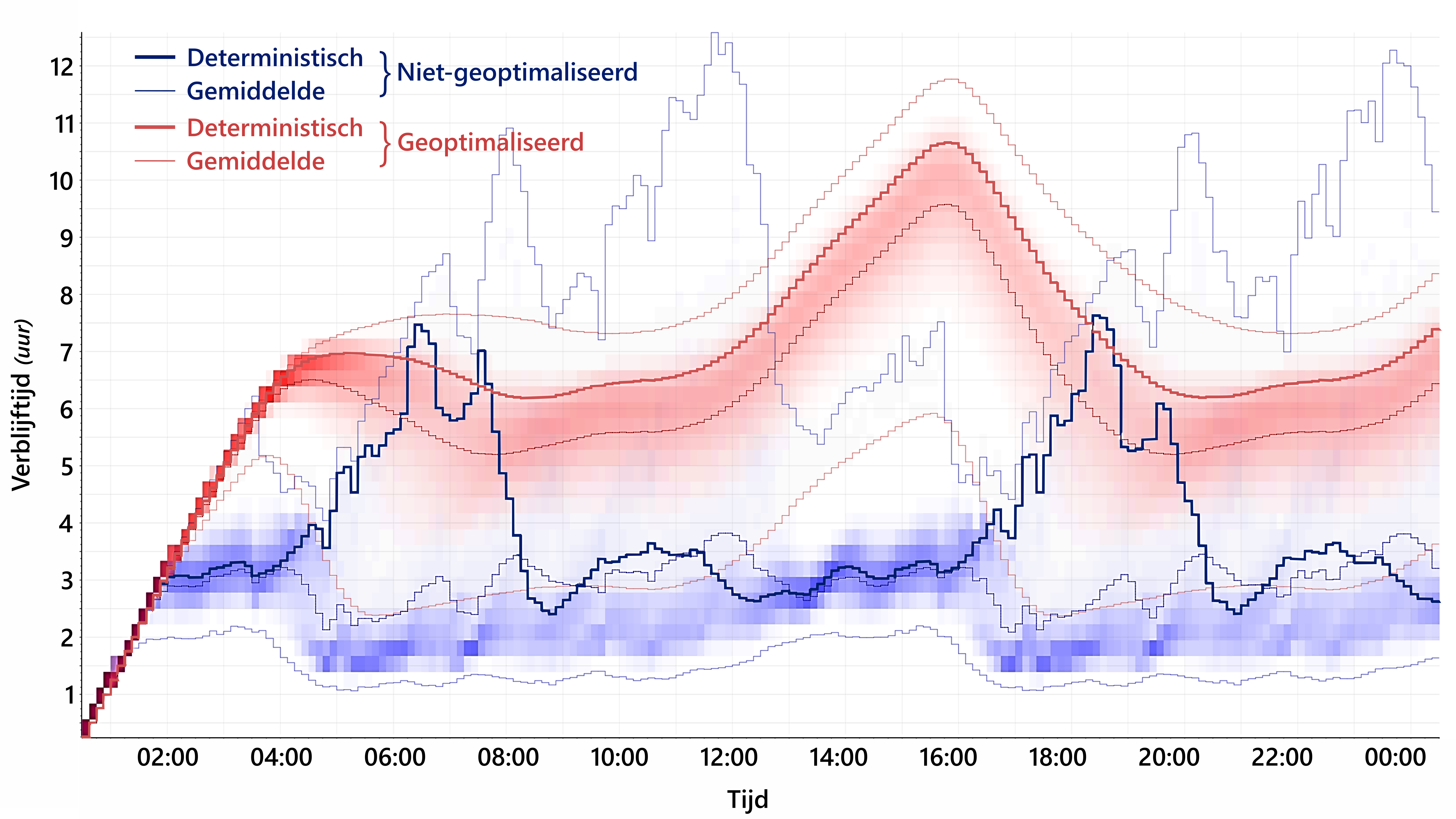
Afbeelding 6. Vergelijking van de verblijftijd van water in het netwerk voor een geselecteerde leiding tussen niet-geoptimaliseerde (blauw) en geoptimaliseerde (rood) modellen
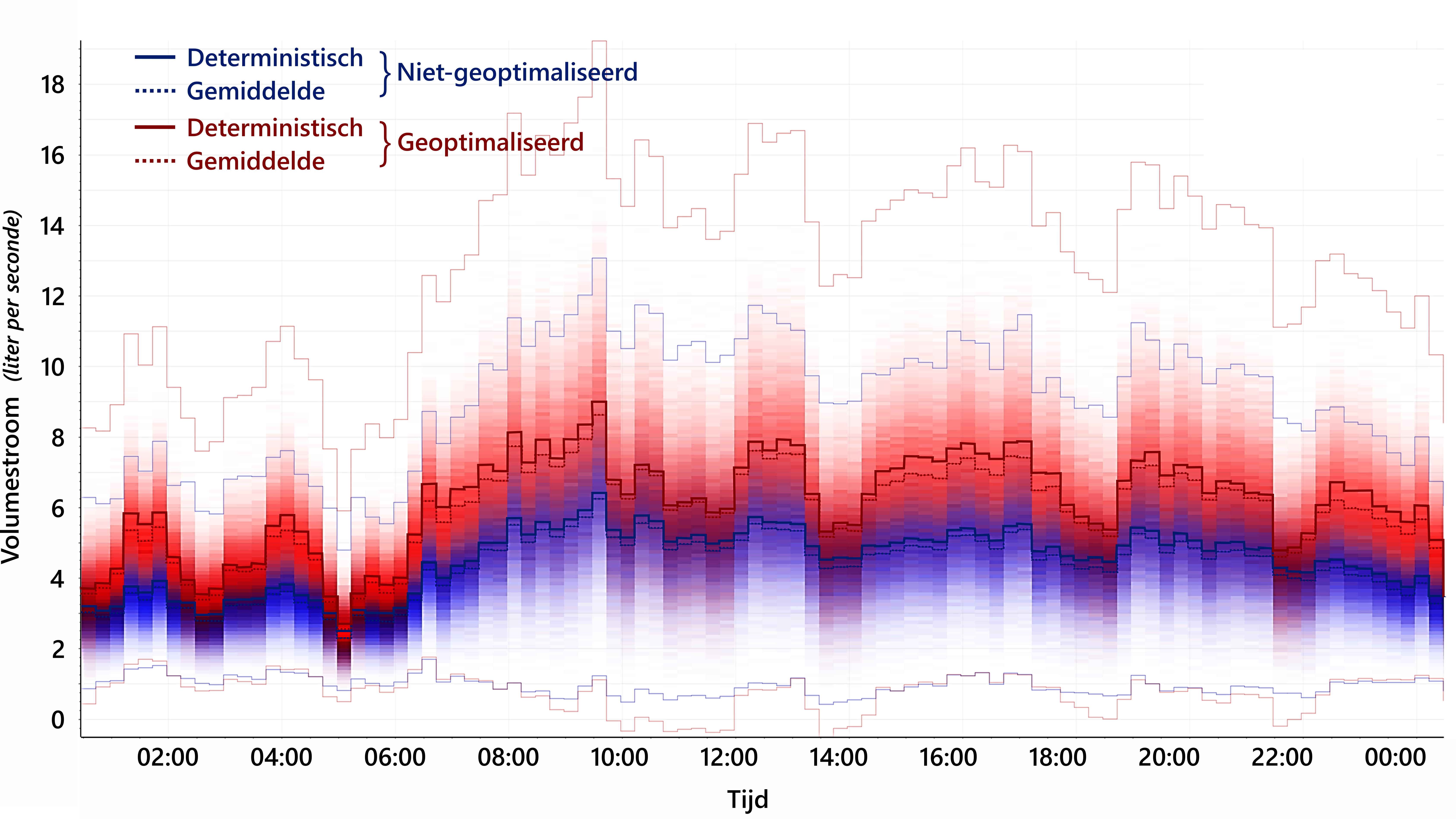
Afbeelding 7. Overlappende onzekerheidsspectra illustreren verandering in stromingsgedrag tussen niet-geoptimaliseerde (blauw) en geoptimaliseerde (rood) modellen
Toegevoegde waarde
De bekende onzekerheden in de invoer van hydraulische modellen zorgen ook voor onzekerheid in de uitkomsten van de berekeningen. Omdat op basis van deze uitkomsten beslissingen worden genomen over ontwerp, onderhoud, en gebruik van het systeem, ontstaat er een risico in deze beslissingen. In de praktijk wordt dit risico meestal opgevangen door voorzichtig te zijn, zoals het overdimensioneren van leidingen 'voor de zekerheid', en door enkele extreme situaties door te rekenen (bijvoorbeeld het maximale waterverbruik op de drukste dag). Maar dit geeft geen garantie dat alle mogelijke problemen, zoals drukproblemen door verouderde leidingen, een per ongeluk gesloten afsluiter, of waterkwaliteitsproblemen worden voorkomen. Daarom is de toepassing van probabilistische simulaties op tal van vlakken mogelijk van toegevoegde waarde. Vertegenwoordigers van drinkwaterbedrijven hebben onder andere de volgende situaties geïdentificeerd, waar leidingnetmodellen kunnen profiteren van probabilistische simulaties:
• waarschijnlijkheid bij voorspellingen ten behoeve van leverings(zekerheids)vraagstukken;
• gevoel voor de bandbreedte van voorspellingen - beter begrip van de betekenis van rekenresultaten;
• ontwerp van het transportnetwerk;
• completer beeld voor de eindgebruikers van hydraulische berekeningen - mogelijkheid tot nuanceren;
• aangeven van onzekerheidsmarges bij berekeningen aan opdrachtgevers/klanten ten behoeve van vertrouwen;
• kalibratie van netwerken, ontwerp, analyses van regulier bedrijf en verstoorde situaties.
Probabilistische simulaties bieden een mate van zekerheid die deterministische simulaties niet kunnen bieden. Er ontstaat een helder beeld van de kwetsbaarheden in het hydraulische model en daarmee ook in de beslissingen die daarop worden gebaseerd. Dit beeld van de kwetsbaarheden kan een waterbedrijf gebruiken om proactief deze kwetsbaarheden te verhelpen, voordat zich situaties voordoen (zoals een verhoogde vraag door hitte) waarin deze kwetsbaarheden tot problemen en dus klachten van klanten leiden. Voorbeelden hiervan zijn een actiever beheer van kritische afsluiters en dimensionering van specifieke leidingen.
Een ander soort vragen
De beschikbaarheid van probabilistische simulatietools zorgt ervoor dat beslissers een ander soort vragen aan modelleurs moeten gaan stellen, en dat zij hierop een ander soort antwoord terug krijgen. Neem als voorbeeld een leiding die voor reparatie moet worden afgesloten, waarbij de wijken in de buurt voldoende druk moeten houden. De vraag die traditioneel gesteld zou worden is: blijft de druk overal in de wijk hoog genoeg als we deze leiding buiten bedrijf nemen? Dit kan deterministisch worden nagerekend, eventueel met een extra scenario voor een verhoogde watervraag omdat er warm weer voorspeld is, en het antwoord dat daaruit komt is ‘ja’ of ‘nee’. Dat lijkt duidelijk, maar er zit, zoals inmiddels bekend, veel onzekerheid verstopt in dit antwoord.
Met een probabilistische simulatie als basis zou de vraag anders moeten worden gesteld, namelijk: wat is de kans dat de druk in de wijk te laag wordt als we deze leiding buiten bedrijf nemen? Het antwoord op die vraag is een berekende kans, waarvan de beslisser vervolgens kan besluiten of deze acceptabel is of niet. Oftewel: dit maakt risicogestuurde besluitvorming over het leidingnet mogelijk.
Uitdagingen
Het uiteindelijke voordeel van de probabilistische aanpak hangt af van de mate van begrip van de grenzen en vorm van de kansverdelingen voor elke onzekere factor. Sommige gegevens, zoals de staat van de leidingen en hun effectieve diameter/ruwheid, zijn moeilijk te verzamelen en te meten. Maar dit neemt niet weg dat er met inspecties en exit-beoordelingen langzaam een bruikbaar beeld kan worden opgebouwd van de variatie in deze parameters. Andere gegevens, zoals de watervraag, kunnen vrij gemakkelijk worden verkregen als de infrastructuur om deze gegevens te verzamelen, zoals slimme meters, beschikbaar is.
De overstap van de ervaren, maar valse, zekerheid van deterministische simulaties naar onzekere probabilistische simulaties kan ongemak oproepen bij gebruikers. Maar er moet ook worden onderkend dat de suggestie van een zeker antwoord (bij deterministische simulaties) niet moet worden vervangen door de suggestie van een zekere kansverdeling (bij een probabilistische simulatie). Beide bieden schijnzekerheid. Niet alle onzekerheid kan worden gevangen in kansverdelingen. Probabilistische simulaties bieden geen volledig en waterdicht beeld van de werkelijkheid. Maar dat komt wel een stap dichterbij.
Perspectief
De theoretische meerwaarde van probabilistische simulaties is duidelijk. De praktische meerwaarde zal in aanvulling hierop moeten worden aangetoond in te praktijk. Wat de auteurs betreft bieden de bovenstaande overwegingen en eerste resultaten ruim voldoende aanleiding om hiermee aan de slag te gaan.
Samenvatting
Besluiten over het gebruik van drinkwaternetten worden veelal gebaseerd op simulaties. Ze gaan echter voor een groot deel voorbij aan de onzekerheden in diverse invoeren van deze modellen. In dit artikel worden een benadering (probabilistische simulaties), een softwarebibliotheek (PHS) en een bureaubladapplicatie (VlinderNET) gepresenteerd, die het mogelijk maken om de hydraulische simulaties uit te voeren met inbegrip van diverse onzekerheden. Het artikel laat zien welke consequenties dit heeft voor modelvoorspellingen van druk, volumestroom en verblijftijd in het leidingnet. Deze ontwikkeling levert een belangrijke bijdrage aan risicogestuurde besluitvorming.
REFERENTIES
1. United States Environmental Protection Agency (2024). EPANET, Application for Modeling Drinking Water Distribution Systems. https://www.epa.gov/water-research/epanet
2. Digital Water Solutions (2024). InfoWorks WS Pro: Collaborative water distribution modelling. https://watersolutions.digital/infoworkswspro/
3. OpenFlows Water (2024). Water Distribution System Modeling and Management. https://www.bentley.com/software/openflows-water/
4. Xu, C. & Goulter, I.C. 1998. ‘Probabilistic Model For Water Distribution System Reliability’. ASCE – Journal of Water Resources Planning and Management. 124(4). doi:10.1061/(ASCE)0733-9496(1998)124:4(218)
5. Vertommen, I., Mitrović, D., Laarhoven, K. van, Piens, P., Torbeyns, M. (2022). ‘Optimization of Water Network Topology and Pipe Sizing to Aid Water Utilities in Deciding on a Design Philosophy: A Real Case Study in Belgium’. Water 2022, 14, 3973. https://doi.org/10.3390/w14233973

















Eerlijker voor de boeren en de maatschappij.